 Problema |
 |
|
Bine ati venit ca musafir! ( Logare | Inregistrare )
HanuAncutei.com - ARTA de a conversa > Odaia Dezbaterilor: Stiinta si Cultura > Exploratorium > Stiinta si Tehnica  |
 26 Jan 2006, 02:58 PM
Mesaj
#1
|
|
 Cronicar  Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862  |
Salutare!
Nu sunt sigur că aici e locul potrivit să postez (dacă nu e... rog moderatorul să mute acest topic; sau sa-l închidă). Am următoarea problemă: Într-o grădină sunt n aspersoare. Pentru fiecare aspersor cunoaştem poziţia lui (x[i],y[i]) şi debitul de apă Q[i] (i = 1..n). Robinetul de alimentare cu apă se află la (x[0],y[0]) şi de-acolo trebuie să tragem o reţea arborescentă de conducte care să distribuie apa la toate cele n aspersoare. Dar trebuie să minimizăm costurile reţelei. Ştim că metrul liniar de conductă are un cost c proporţional cu radicalul debitului pe care-l suportă acea conductă: c = k*sqrt(Q). Deci dacă pe o anume distanţă două tronsoane de debite Q1 şi Q2 se pot contopi într-un singur tronson de debit Q1+Q2, costul va fi mai mic (radicalul sumei e mai mic de cât suma radicalilor). Întrebarea e: care ar fi un algoritm pentru determinarea arborelui de cost minim? Iată o schiţă explicativă:  În imagine se văd conductele mai groase (şi mai scumpe) care cumulează mai mult debit, pe care apoi îl împart către conducte tot mai subţiri, către consumatorii finali. Am considerat că toţi consumatorii au acelaşi debit -- e o simplificare OK pentru o primă abordare. (Evident, problema e teoretică -- aspersoarele şi grădina sunt doar metafore.) Are cineva ceva idei? a -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
 |
 
|
|
26 Jan 2006, 03:48 PM
Mesaj
#2
|
|
|
Cronicar Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862 |
Problema poate fi reformulată şi astfel:
N călători pleacă împreună de la "sursă", fiecare trebuind să ajungă în final la câte o destinaţie (x[i],y[i]). Costurile călătoriei împreună sunt mai mici decât costurile călătoriei de unul singur: pentru un grup, costul pe metru liniar este proporţional cu radical din numărul membrilor grupului. Grupul mare iniţial înaintează, dar la un moment dat devine mai eficient ca el să se rupă în două grupuri mai mici, care-şi continuă călătoriile în direcţii diferite. Sub-grupurile se împart apoi în sub-sub-grupuri şi tot aşa, până când se fărâmiţează în indivizi care-şi parcurg fiecare singur ultima porţiune până la destinaţie. Care-i algoritmul după care decidem când şi cum trebuie rupte grupurile pe parcurs, astfel încât costul călătoriei să fie minim pentru fiecare participant? (Errr... O fi echivalentă formularea asta cu cea iniţială? Trebuie arătat...) a -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
|
|
|
|
26 Jan 2006, 03:59 PM
Mesaj
#3
|
|||
 Domnitor Grup: Membri Mesaje: 1.849 Inscris: 30 March 04 Din: Timisoara Forumist Nr.: 2.824 |
Cred ca nu. O calatorie implica existenta unor cai de comunicatie pe care trebuie sa le urmam, pe cand in prima formulare, alegerea pozitiei conductelor se face "la liber". -------------------- Suntem ceea ce gândim. (Buddha)
|
||
|
|
|
||
| Promo Contextual |
26 Jan 2006, 03:59 PM
Mesaj
#
|
 ContextuALL |
|
|
|
|
|
26 Jan 2006, 04:34 PM
Mesaj
#4
|
|
|
Domnitor Grup: Membri Mesaje: 1.849 Inscris: 30 March 04 Din: Timisoara Forumist Nr.: 2.824 |
Pentru rezolvare, cred ca ar fi bine sa reducem problema la 2 aspersoare si un robinet.
PS: N-am reusit nici macar asa sa o rezolv 
-------------------- Suntem ceea ce gândim. (Buddha)
|
|
|
|
|
26 Jan 2006, 04:34 PM
Mesaj
#5
|
|
|
Cronicar Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862 |
"Călătoria" e pe o câmpie unde nu există trasate drumuri (înaintarea în orice direcţie costă la fel de mult, contează doar asocierea sau nu cu alţi călători).
Între timp, cred că am găsit singur soluţia la problema cu "călătoria". Algoritmul ar fi aşa: Pornesc cei N oameni în grup, pe direcţia "centrului de masă" al punctelor de destinaţie. Direcţia aceasta împarte destinaţiile (şi deci călătorii) în două categorii: unele destinaţii se află la dreapta direcţiei curente, altele la stânga. În fiecare moment determinăm ce-i mai ieftin: a. subgrupurile "de dreapta" şi "de stânga" rămân unite şi mai fac împruenă un pas ds pe direcţia centrului comun de masă, sau b. subgrupurile "de dreapta" şi "de stânga" se despart şi fiecare o ia spre centrul de masă al destinaţiilor "de dreapta", respectiv "de stânga", înaintând cu câte un pas ds pe aceste direcţii. Dacă b e mai ieftin, se produce ruptura. Şi algoritmul se reia pentru fiecare subgrup în parte. Pentru ponderi egale ale destinaţiilor (debite egale în prima formulare), am impresia că totul se reduce la o socoteală de unghiuri: când direcţia către centrul de masă "de dreapta" (sau "de stânga") face un anume unghi cu direcţia către centrul de masă comun, atunci se produce ruptura:  Ei? a -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
|
|
|
|
26 Jan 2006, 04:41 PM
Mesaj
#6
|
|
 Domnitor Grup: Membri Mesaje: 5.298 Inscris: 9 June 04 Forumist Nr.: 3.787 |
Si centrul de masa cum il afli?
-------------------- viata e simpla si misto!
|
|
|
|
|
26 Jan 2006, 04:43 PM
Mesaj
#7
|
|
|
Cronicar Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862 |
Păi... media coordonatelor.
a EDIT: Media ponderată cu "importanţele" Q[i], dacă ele sunt diferite. Acest topic a fost editat de Amenhotep: 26 Jan 2006, 04:55 PM -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
|
|
|
|
26 Jan 2006, 05:15 PM
Mesaj
#8
|
|
 Umil servitor la Han Grup: Moderator Mesaje: 4.051 Inscris: 2 December 03 Forumist Nr.: 1.345 |
Pentru debite egale, parerea mea este ca avem de-a face o o problema clasica de drum minim (cost minim)
Se rezolva cu grafuri, mai exact cu arbori... Cred totusi ca la sfarsit drumul va arata cam asa (cu verde), caci in opinia mea acesta este mai eficient, si evident conducta va pleca cu un anumit diamentru si pe masura ce va lasa in urma un nod, se va reduce cu un coeficient, oarecum usor de determinat..(in functie de numarul nodurilor ramase)  In cazul unor debite neegale (de valori diferite mult), atunci este o idee cu calcularea centrului de greutate... Niste teorie si algoritmi, care e posibil sa te ajute, gasesti aici: Link1 Link2 -------------------- Gandurile Mele nu sunt ca gandurile voastre si caile Mele ca ale voastre, zice Domnul.
Si cat de departe sunt cerurile de la pamant, asa de departe sunt judecatile Mele de judecatile voastre si cugetele Mele de cugetele voastre. (Isaia 55:8.9) Ortodoxia - Calea intru Hristos - pe pagina 1 indexarea tematica a subiectelor pt. o usoara urmarire... |
|
|
|
|
26 Jan 2006, 07:24 PM
Mesaj
#9
|
|
|
Cronicar Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862 |
Da Clopoţel, ai dreptate, există algoritmi de găsire a unui drum optim într-un graf.
Dar mie îmi trebuie neapărat ca graful să fie un arbore! Adică nodurile cele negre trebuie să fie frunze: o conductă nu are voie să vină şi apoi să plece de la un nod. Şi, în plus, nici nu se ştie de la început structura grafului (asta trebuie determinat). Adică, de exemplu, nu se ştie care dintre cele două variante trebuie aleasă:  Aşadar, în problema de faţă nu există un graf de la care pornim (şi în interiorul căruia să trebuiască să rezolvăm o problemă de minim), ci problema este exact construirea arborelui având frunze şi rădăcină fixate. (Dacă această problemă o rezolvăm cumva -- deci dacă ajungem să ştim structura arborelui --, atunci problema de optim devine simplă: n-avem decât să exprimăm costul total ca funcţie de poziţiile nodurilor variabile şi apoi determinăm minimul acestei funcţii.) În concluzie, eu n-am putut găsi în teoria grafurilor nimic care să m-ajute... a Acest topic a fost editat de Amenhotep: 26 Jan 2006, 07:30 PM -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
|
|
|
|
26 Jan 2006, 10:27 PM
Mesaj
#10
|
|
 Filosof boem Grup: Membri Mesaje: 6.222 Inscris: 10 July 03 Din: Bucuresti Forumist Nr.: 445 |
Ok, problema in varianta redusa, cu o sursa si 2 aspersoare poate fi formulata in felul urmator: avem un triunghi cu varfurile in cele 2 aspersoare si in sursa. Notam laturile cu a, b, c. Trebuie sa gasim punctul O unde conducta mare de la sursa se imparte in 2. Notam cu a1, b1, c1, lungimile segmentelor de la O la cele 3 varfuri.
Problema se formalizeaza in felul urmator Sa se determine min(a1*sqrt(2)+b1+c1) //am presupus ca a1 este conducta care pleaca din sursa cu conditiile triunghi(a,b,c) triunghi(c,a1,b1) triunghi(a,b1,c1) triunghi(b,a1,c1) unde triunghi(a,b,c) se transcrie in a<=b+c, b<=a+c, c<=a+b Aceasta este o problema foarte complexa la prima vedere. In realitate este o problema clasica de optimizare liniara pentru care exista un algoritm, algoritmul simplex (se gasesc implementari ale lui in toate programele mari specializate pe matematica sau statistica si probabil si implementari de sine statatoare pe net). Insa cand se pune problema generalizata... nu stiu, nu mi-a venit inca nici o idee. Poate va vine voua.  Totul e sa gasim punctul in care se desparte prima conducta mare cumva. Dup-aia e o simpla problema de inductie generalizata.P.S. Amenhotep, problema asta ai inventat-o tu sau ai gasit-o pe undeva? Edit: nu prea cred sa aiba vreo legatura centrul de masa in toata afacerea asta... asta ar insemna ca din simplexul ala sa ti se simplifice cumva radical din 2-ul ori din experienta mea asa ceva nu are cum sa se intample. Acest topic a fost editat de Catalin: 26 Jan 2006, 11:53 PM -------------------- A nation cannot prosper for long when it favors only the prosperous - Obama
|
|
|
|
|
27 Jan 2006, 12:57 AM
Mesaj
#11
|
|
|
Filosof boem Grup: Membri Mesaje: 6.222 Inscris: 10 July 03 Din: Bucuresti Forumist Nr.: 445 |
Cred ca am gasit si o solutie la cazul general:
Avem o sursa si N aspersoare. Asta inseamna un arbore binar cu N frunze si radacina in sursa. Cati arbori binari avem cu N frunze si radacina fixa? 2^(N-1) - 1 (demonstratia e simpla prin inductie, n-o fac aici). Deci avem 2^(N-1)-1 structuri posibile de arbori. Fiecare structura are un minim propriu, calculabil printr-un simplex similar cu cel la cazul N=2, dar cu inecuatii mai complicate. Fiecare inecuatie va reflecta existenta unei anumite linii poligonale (de exemplu, in figura de mai jos, relatia subliniata va fi d(X,Y)<=suma lungimilor celorlalte 5 laturi - X si Y sunt varfurile respective. Dupe ce scriem toate relatiile, o sa avem (N+1)*N/2 inecuatii si o anumita functie de minimizat care va arata ceva de genul a1*sqrt(N)+b1*sqrt(N-1)+... Insa totul fiind liniar, se aplica algoritmul simplex si problema se rezolva. Dupa ce calculam pentru toate cele 2^(N-1)-1 cazuri, luam minimul absolut dintre ele si obtinem raspunsul la problema. 
-------------------- A nation cannot prosper for long when it favors only the prosperous - Obama
|
|
|
|
|
27 Jan 2006, 01:05 AM
Mesaj
#12
|
|||||||
|
Cronicar Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862 |
Da, aşa e pt. 2 puncte. Cu observaţia că dpdv geometric condiţiile se reduc la: punctul O să fie în interiorul triunghiului (pentru orice soluţie cu O în afara triunghiului, se poate arăta că există o soluţie mai bună cu O în interiorul triunghiului). Am exprimat în funcţie de coordonatele x şi y ale lui O, am derivat şi am găsit minimul. Nu mai ştiu soluţia analitică, dar parcă-i găsisem şi o interpretare geometrică frumoasă.
Păi eu m-am gândit aşa: dacă cele n puncte sunt grupate în două aglomerări distincte şi pornim de undeva departe, acele două aglomerări pot fi aproximate prin centrele lor de masă (din origine "se văd" ca două puncte). Şi tratăm problema ca şi cum am avea doar două aspersoare (de debite diferite, date de numărul de aspersoare din fiecare aglomerare). După ce ţeava cea mare s-a despărţit în două, pentru fiecare ţeavă repetăm algoritmul -- până când se apropie suficient de mult de aglomerare încât "să distingă" două sub-aglomerări diferite, una de-a stânga şi una de-a dreapta centrului lor comun.
Nu am găsit-o nicăieri. Mi-e şi jenă să spun de unde provine... Am vrut să generez automat nişte poze cu neuroni. Şi mi-am pus problema cum construiesc automat un neuron arborescent "frumos" care duce la n sinapse poziţionate aleator prin spaţiu. Studiind eu poze de neuroni pe web, am observat că dintr-un trunchi gros se desprind ramuri mai subţiri, din care se desprind ramuri şi mai subţiri şi tot aşa. Am căutat un fenomen fizic care să semene cu aşa ceva şi mi-a venit ideea unui sat ale cărui case trebuie alimentate cu apă (aici am formulat cu aspersoare în grădină, dar iniţial aşa mă gândisem, cu case într-un sat). Condiţia cu sqrt(Q) provine din aceea că ceea ce plăteşti la conductă e metalul din care-i făcută -- deci proporţional cu perimetrul secţiunii, nu cu aria ei (dar debitul e proporţional cu aria). Cam asta-i geneza problemei...OK, acum, dacă tot v-am zis de unde provine... ar mai fi o restricţie: în fiecare "aspersor" ştim nu doar debitul, ci şi unghiul (direcţia) sub care trebuie să sosească apa. Iar conductele trebuie să aibă curburi cât mai line (nu bruşte). Şi conductele mai groase sunt mai puţin flexibile decât alea subţiri. Asta face ca traseele să nu mai fie linii drepte. Trunchiul principal va porni pe o anume direcţie din sursă şi se va curba greu ("încăpăţânat") înspre sinapse. Fiecare rămurică se va curba mai uşor. Şi ele se vor sfârşi în aşa fel încât să facă buton sinaptic frumos, perpendicular pe diverse suprafeţe date (care suprafeţe... aparţin unor neuroni deja construiţi, aţi ghicit! ).a PS: Iată, o imagine de genul ăsta aş vrea să generez: 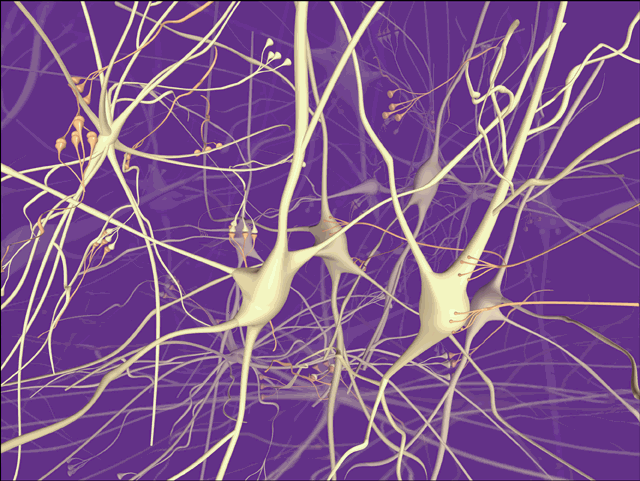 Sau poate aşa:  Sau:   EDIT: Deci problema cea mai generală e: Dată fiind o rădăcină (ca versor: poziţie + direcţie) şi n frunze (tot ca versori: poziţie + direcţie), cum construim un arbore care să arate cât mai "organic", cât mai natural, cât mai frumos? Care să sugereze cât mai bine ideea că "ceva" este distribuit în mod economic la cele n frunze? Acest topic a fost editat de Amenhotep: 27 Jan 2006, 01:16 AM -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
||||||
|
|
|
||||||
|
27 Jan 2006, 08:59 AM
Mesaj
#13
|
|
 Domnitor Grup: Membri Mesaje: 6.255 Inscris: 3 October 03 Forumist Nr.: 899 |
Suna a problema de optimizare. In nici un caz a problema de grafuri (arbore minim de acoperire sau ceva asemanator). Asa ca s-ar putea sa merite sa cauti o formulare in LP sau QP.
-------------------- Azi avem.
 |
|
|
|
|
27 Jan 2006, 05:25 PM
Mesaj
#14
|
|||
|
Cronicar Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862 |
Ce înseamnă LP sau QP?
Mă tot gândeam care sunt variabilele în funcţie de care faci tu optimizarea... şi cum interacţionează ele liniar (încât să poţi aplica algoritmul simplex)... Şi abia acum mi-am dat seama: tu consideri că a1, b1 şi c1 sunt variabilele! Dar nu-i aşa, ele nu sunt independente, dacă fixezi pe a1 şi b1, atunci c1 nu mai rămâne să varieze în vreun interval, ci e condamnat să ia doar una din două valori posibile. Eu zic că problema nu se poate rezolva cu metoda simplex. Pentru că nu avem dependenţă liniară. În altă ordine de idei, mi-am dat seama că nici propunerea mea cu centrul de masă nu merge. Iată un exemplu:  Conform algoritmului prezentat de mine mai sus, călătorul care are ca destinaţie punctul indicat va opta la început s-o ia pe ramura din stânga. Deci după despărţirea de prietenul său care rămâne la căsuţa din stânga jos, va fi obligat să parcurga tot drumul până sus de unul singur. Or, este evident că ar fi mai avantajos să meargă cu grupul de dreapta... Aşadar... back to square one. a Acest topic a fost editat de Amenhotep: 27 Jan 2006, 05:43 PM -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
||
|
|
|
||
|
27 Jan 2006, 05:35 PM
Mesaj
#15
|
|
|
Filosof boem Grup: Membri Mesaje: 6.222 Inscris: 10 July 03 Din: Bucuresti Forumist Nr.: 445 |
LP e programare liniara, m-as miza!
Adica ce ziceam eu cu simplex. -------------------- A nation cannot prosper for long when it favors only the prosperous - Obama
|
|
|
|
|
27 Jan 2006, 06:25 PM
Mesaj
#16
|
|
|
Cronicar Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862 |
Errr... Şi QP atunci ce să fie? Quick Programming?
a -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
|
|
|
|
27 Jan 2006, 06:35 PM
Mesaj
#17
|
|
|
Domnitor Grup: Membri Mesaje: 6.255 Inscris: 3 October 03 Forumist Nr.: 899 |
LP = linear programming
Ai sistem de ecuatii liniare QP = quadratic programming -------------------- Azi avem.
|
|
|
|
|
27 Jan 2006, 06:42 PM
Mesaj
#18
|
|
|
Cronicar Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862 |
Dar care sunt ecuaţiile liniare? Am arătat că nu sunt ecuaţii liniare (între nişte variabile independente), ci variabilele sunt legate prin ecuaţii neliniare...
a -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
|
|
|
|
27 Jan 2006, 08:45 PM
Mesaj
#19
|
|||||
|
Umil servitor la Han Grup: Moderator Mesaje: 4.051 Inscris: 2 December 03 Forumist Nr.: 1.345 |
Dragii mei, Personal, mie problema mi se pare interesanta si utila, deoarece in curand vine primavara si trebuie sa ud si eu gradina...
Parerea mea este ca totusi, ideea cu centrul de masa este buna, numai ca trebuie putin adaptata..... Iata la ce ma refer: - in loc de masa, evident avem debit, notam aceasta valoare cu d - sursa are valoarea = suma tuturor debitelor punctelor - sursa este nod in arbore si este chiar nodul 1 - propun urmatoarele notatii: n - numarul de noduri x,y - coordonatele SX=suma de la i=1 la n din xi*di SY=suma de la i=1 la n din yi*di D = suma de la i=1 la n din di X = SX/D Y = SY/D - dupa ce calculam asta, trasam (prelungim) conducta (cu diametrul initial) din nodul 1(sursa) in acest punct de coordonate X,Y - calculam distanta de la acest punct la nodul cel mai apropiat (excluzandu-l pe 1 evident) (nodul 2) - trasam o conducta de debit d2 la la (X,Y) la nodul 2 - se recalculeaza: D=D-d2 punctul de coordonate (X,Y) devine acum nodul 1, adica sursa, si se exclud din calcule atat sursa initiala cat si nodul 2 prin urmare se recalculeaza X si Y in noile conditii Banuiesc ca in doua cicluri for sau while avem coordonarele tuturor punctelor conductei Evident ca la pasul n-2 (asa mi se pare la prima ochire) algoritmul se opreste caci toate datele sunt obtinute... Cred ca va merge... Adica acum nu vad nici un motiv sa nu mearga... Daca gasiti voi vreunul, sa-mi spuneti si mie, sa nu tai tevile degeaba...
E...aici e alta treaba, ca ce am vorbit noi mai sus nu are treaba cu frumosul ci cu eficientul Daca vrei frumos, atunci iti recomand cu caldura sa generezi acest "neuron arborescent frumos" cu ajutorul fractalilor... O sa ai posibilitatea sa setezi si unghiuri si multe alte chestii... Parerea mea... -------------------- Gandurile Mele nu sunt ca gandurile voastre si caile Mele ca ale voastre, zice Domnul.
Si cat de departe sunt cerurile de la pamant, asa de departe sunt judecatile Mele de judecatile voastre si cugetele Mele de cugetele voastre. (Isaia 55:8.9) Ortodoxia - Calea intru Hristos - pe pagina 1 indexarea tematica a subiectelor pt. o usoara urmarire... |
||||
|
|
|
||||
|
28 Jan 2006, 01:25 AM
Mesaj
#20
|
|||||||||||
|
Cronicar Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862 |
Deci ducem o conductă groasă până în "centrul de debit" (centrul de masă ponderat cu debitele). OK, înţeleg.
Deci ducem apoi o conductă subţire până la cel mai apropiat consumator. Pe urmă probabil că ne întoarcem în "centrul de debit"... cred (că altfel n-am mai avea de unde să dăm debit celorlalţi consumatori). Corect?
Aici m-ai pierdut complet. Cum o să devină (X,Y) sursa? Şi de ce ai notat sursa ca fiind nodul 1 şi nu nodul 0, cum am formulat eu problema? Dacă sursa e nodul 1 atunci ai doar n-1 aspersoare...
Nu ştiu dacă merge sau nu, pentru că nu am înţeles propunerea ta. Poţi te rog să exemplifici pe cazul acesta foarte simplu?  Eu am găsit că costul minim pentru instalaţia din figură este 42,42 lei (când conducta groasă merge 10 metri şi apoi se ramifică). Dacă tu propui ca această conductă groasă să meargă până în "centrul de debit" al consumatorilor (care se află la jumătatea distanţei dintre cei doi consumatori)... vei obţine un cost mai mare (48,28 lei). Încă o întrebare: în figura de mai sus, algoritmul propus de tine este influenţat de distanţa orizontală dintre cei doi consumatori? Adică, dacă de exemplu cei doi consumatori de îndepărtează simetric cu încă 10 metri fiecare (distanţa dintre ei ajungând 40 de metri), ce rezultat dă algoritmul tău? Eu spun că în acest caz cel mai mic cost se obţine cu un "arbore" în formă de V: adică din sursă pleacă direct conducte subţiri către cei doi consumatori, fără să mai existe conductă groasă -- şi costul minim este 56,56 lei. Algoritmul tău ce zice?
Sunt foarte interesat de orice sugestii. Cum crezi că pot genera cu ajutorul fractalilor un arbore ale cărui frunze să fie cele din figura de mai jos, de exemplu?  Închipuie-ţi că acolo a fost desenat un arbore (neuron) frumos şi cineva a şters ramurile, lăsând doar sinapsele şi nişte indicii despre direcţia din care veneau ramurile. Şi eu acum trebuie să refac arborele, pornind din rădăcina albastră şi ajungând în fiecare sinapsă roşie, conform direcţiilor indicate. Încât să arate cât mai natural. Cum rezolv asta cu ajutorul fractalilor? a -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
||||||||||
|
|
|
||||||||||
|
28 Jan 2006, 02:20 AM
Mesaj
#21
|
|||
|
Domnitor Grup: Membri Mesaje: 6.255 Inscris: 3 October 03 Forumist Nr.: 899 |
Ai fii uimit sa vezi cate probleme se pot reduce la o problema de LP de exemplu. Apoi, nu trebuie sa o reduci neaparat la LP. Exista algoritmi sa rezolvi si alte tipuri de probleme decat cele exprimate prin [in]ecuatii liniare. In nici un caz, abordari ca cele cu centru de masa sau ca cele a-la Glopotel nu cred ca vor merge vreodata. Nu este o problema banala. Spatiul de cautare al solutiei as spune ca este foarte mare. -------------------- Azi avem.
|
||
|
|
|
||
|
28 Jan 2006, 10:59 AM
Mesaj
#22
|
|||||||||||||||||||||
|
Umil servitor la Han Grup: Moderator Mesaje: 4.051 Inscris: 2 December 03 Forumist Nr.: 1.345 |
Draga Amenhotep, Imi cer scuze ca nu am fost prea clar in exprimare....
Da, asta am spus, caci in sursa nu se reduce debitul..., acolo neavand consumator...
Corect, caci acela este minimul local si trebuie profitat de el Atentie: Te rog sa observi, ca, coordonatele punctului sursa sunt foarte importante, si deci trebuie luate in calcul....
Corect, si algoritmul se reia plecand acum de la faptul ca noul "centru de debit" este acum sursa, si se reduc consumatorii cu 1. Atentie: daca de la "centrul de debit" exista mai multi consumatori, aflati la distante egale de el, atunci se traseaza toate(casi sunt minime locale), si apoi se reduce numarul consumatorilor corespunzator..., la fel si debitele...
Pai nu devine noul punct, noua sursa pentru punctele ramase? Ce ai lasat in urma este deja trecut...
Scuze... am omis ca ai notat sursa cu 0... E chestiune de notatie... Poti la fel de bine sa pleci si cu sursa ca fiind nodul 1  , sau 10..., sau a, x... (oricum definesti siruri de genul n[i])
Eu m-am gandit, ca pentru o implementare mai usoara a algoritmului, sa consideri si sursa ca nod, pentru calcularea centrului de masa...Iar in calculul consumului, consumul acesteia ar fi =0...deci debitul ramane neschimbat dupa el...
Eu nu am propus deloc ca, conducta groasa sa mearga pana in "centrul de debit" al consumatorilor... Ar fi o eroare matematica.... Deci, mie mi se pare ca treaba e foarte simpla: In figura ta, avem un triunghi in care varful de jos e sursa... Nu trebuie decat sa-i calculezi centrul de masa ca la geometrie, dar modificat putin cu formulele ce ti le-am dat, caci intervine debitul....(adica, ca si cum, distantele ar fi influentate de ponderile consumului)
Nu, e cam gresit ce spui... Matematic, ca sa fie eficient, sa plece ambii consumatori chiar din sursa, in forma de "V", ar trebui ca acestia sa fie situati la infinit unul de altul... Cand centrul de masa al unui triunghi este chiar intr-un varf al lui? Cand celelalte doua varfuri ar fi situate pe aceeasi dreapta cu el, dar de parti diferite? Cand centrul de masa al unui triunghi cade chiar la mijlocul segementului dintre doua varfuri? Cand doua varfuri sunt situate in acelasi punct, adica suprapuse... Algoritmul,asa cum l-am dat eu, functioneaza si in cazul general si in cazuri particulare, cu debite egale, dar si cu debite exagerat de diferite... Te rog sa-l analizezi mai atent... Observatie: Algoritmul este teoretic...Practic, evident, mai intervin multe lucruri, cum ar fi: numarul de imbinari (reductii), coturi, suporti, prinderi etc, care sunt foarte scumpe... Deci e alta mancare de peste... Evident, se pot introduce si acestea in algoritm si atunci o sa avem (poate), un traseu cu totul diferit decat cel ce nu le ia in calcul...
Eu nu am mai lucrat cu fractalii de vreo 8 ani... Reusisem sa fac lucruri destul de complexe cu ei... Sunt buni la modelarea unor forme naturale, cum ar fi chiar arborii sau neuronii, si permit chiar reglaje sensibile... O sa ma uit pe documentatiile mele si o sa-ti trimit ceva, chiar si niste surse in Pascal/Delphi...Dar, ai putea sa cauti pe internet, sunt convins ca vei gasi mult mai multe documentatii de fractali, chiar surse de programe si chiar generatoare de fractali, gata facute... E fantastic... Eu m-am rupt de ceva ani de treaburile astea si mi-am pierdut indemanarea ... Vorbesc din aduceri aminte.... 
Ok...daca nu e foarte urgent, o sa ma straduiesc sa-ti fac un program in Delphi, care sa genereze forme asa cum le vrei tu... Acest topic a fost editat de Clopotel: 28 Jan 2006, 11:05 AM -------------------- Gandurile Mele nu sunt ca gandurile voastre si caile Mele ca ale voastre, zice Domnul.
Si cat de departe sunt cerurile de la pamant, asa de departe sunt judecatile Mele de judecatile voastre si cugetele Mele de cugetele voastre. (Isaia 55:8.9) Ortodoxia - Calea intru Hristos - pe pagina 1 indexarea tematica a subiectelor pt. o usoara urmarire... |
||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
28 Jan 2006, 12:55 PM
Mesaj
#23
|
|||||||||||||||||||||||
|
Cronicar Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862 |
OK, acum am înţeles algoritmul. Problema cu el e că nu conduce la soluţia optimă. De exemplu, pentru problema simplisimă cu doi consumatori egali, "centrul de debit" se află la mijlocul distanţei dintre ei. Deci algoritmul tău prescrie un arbore în formă de T:  Or, am arătat mai devreme că există o configuraţie cu cost total mai mic (configuraţia Y, cu cost 42,42 lei). Deci algoritmul tău nu conduce la cel mai mic cost.
Asta e clar.
Hmm... Acum dintr-o dată nu mai e clar.
OK, cât e ponderea consumului în vârful de jos al triunghiului? Zero (căci acolo nu se consumă, cum însuţi tu ai remarcat). Deci coordonatele acelui vârf vor veni înmulţite cu zero în formulele tale. Deci el nu contează. Mai rămân celelalte două vârfuri, care au ponderi (consumuri) egale -- deci conform formulelor tale "centrul de debit" va rezulta la mijlocul distanţei dintre cei doi consumatori.
Păi vezi? Exact ce-ţi spuneam: algoritmul tău nu va ajunge niciodată la configuraţia în formă de V, ci va recomanda mereu o altă configuraţie, cu cost mai mare decât aceea în formă de V (care este configuraţia de cost minim -- dacă crezi că nu-i aşa, încearcă să găseşti o configuraţie cu cost mai mic de 56,56 lei!): 
L-am analizat pe cele două cazuri particulare foarte simple prezentate mai sus. Şi am remarcat că acel algoritm conduce la soluţii cu cost mai mare decât costul găsit de mine ca fiind minim. Deci algoritmul nu e bun, pentru că nu dă soluţia optimă.
Dar eu ştiu bine ce sunt fractalii şi care-i treaba cu ei. Problema nu e că n-am documentaţie despe fractali, ci că nu văd cum ei m-ar putea ajuta în problema pe care-o am: construirea unui arbore când se dau frunzele şi rădăcina.
Mi-ar fi de folos doar algoritmul, nu consuma timp scriind programul pentru mine (deşi... rularea programului e cea mai bună dovadă că algoritmul chiar funcţionează ).a -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
||||||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
28 Jan 2006, 01:46 PM
Mesaj
#24
|
|||||||
|
Cronicar Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862 |
În cazul de faţă, mi-ar folosi cel mai mult uimirea de a vedea cum această problemă poate fi redusă la una de LP...
OK, care este (in)ecuaţia (sau sistemul de (in)ecuaţii) pentru problema de faţă? Pentru problema simplă cu doar doi consumatori, dacă plecăm de la distanţele a1, b1 şi c1 definite de Cătălin, eu zic că avem: a1 >= 0 b1 >= 0 c1 = distanţa de la vârful C la intersecţia/intersecţiile celor două cercuri de raze a1 şi b1, cu centrele în A, respectiv B:  Rezultă o ecuaţie de gradul 2 pentru c1, ecuaţie ce poate avea 0, 1 sau 2 soluţii. OK, asta-i pentru 2 consumatori. Dar pentru n consumatori? Mie-mi pare că apar ecuaţii de grad din ce în ce mai mare, între tot mai multe variabile... Deci cum propui să abordăm problema?
Sunt de aceeaşi părere. Aseară mi-a venit însă o idee: Să considerăm nişte fire care la început leagă sursa direct cu fiecare consumator, în linie dreaptă. Adică e ca un fel de stea, de mănunchi de fire drepte care duc direct la consumatori. Bun, acum să ne imaginăm că firele astea sunt nişte elastice tensionate. Şi să ne mai imaginăm că ele se atrag gravitaţional. Adică un element de lungime ds dintr-un fir se atrage cu toate celelalte elemente de lungime ds din celelalte fire (dar nu şi cu cele din firul propriu). Pentru simplitate, să discretizăm: "firele" sunt de fapt şiruri de biluţe legate cu resorturi. Şi fiecare biluţă se atrage gravitaţional cu toate celelalte biluţe (mai puţin cele de pe firul propriu), cu o forţă invers proporţională cu pătratul distanţei. (Ca să nu ajungem la forţe infinite, putem considera că două biluţe nu se pot apropia la mai mult de distanţa epsilon.) Ei bine, eu intuiesc că lăsând acest sistem să se mişte sub acţiunea forţelor care apar, el se va stabiliza într-o configuraţie care este exact cea căutată. Două fire care converg spre sursă vor avea tendinţa de a se lipi unul de altul. Dar aceasta va conduce la întinderea lor, deci elasticitatea resorturilor le va face să nu se lipească decât până la un punct. Apoi, un "trunchi" gros de fire deja lipite va exercita o atracţie mare asupra unor fire izolate aflate prin preajmă şi le va trage spre el. Astfel, simulând dinamica unui astfel de sistem de "fire grele", eu zic că s-ar putea să obţinem soluţia... În plus, dacă introducem şi o "rezistenţă la încovoiere", firele nu vor mai fi drepte, ci se vor curba. Şi trunchiurile groase se vor curba mai greu decât firele subţiri. Deci vom putea impune şi anumite direcţii la consumatori, respectiv la sursă. Ce ziceţi de abordarea asta? a -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
||||||
|
|
|
||||||
|
28 Jan 2006, 04:10 PM
Mesaj
#25
|
|||||
|
Umil servitor la Han Grup: Moderator Mesaje: 4.051 Inscris: 2 December 03 Forumist Nr.: 1.345 |
Draga Amenhotep, Dupa cum vezi nu am talent la explicatii ca nu ma pot face inteles... O sa reformulez altfel...
Nu, nu vei inmulti cu zero niciodata cand vei calcula coordonatele, caci acolo nu intervine consumul ci doar debitul ce trece prin nod... Poate doar cand calculezi debitele urmatoare, pentru simplitatea algoritmului cand e vorba de calculul consumului in centrul de masa inmultesti cu zero... Din contra, in punctele "sursa" debitul D= suma debitelor nodurilor nealimentate inca.... Deci in cazul simplu al triunghiului tau avem formulele: D0= d1+d2 Xcm = (d0*x0+d1*x1+d2*x2)/(d0+d1+d2) Ycm = (d0*y0+d1*y1+d2*y2)/(d0+d1+d2) si astfel avem pozitia centrului de masa... Aici trebuie sa punem un distribuitor cu reductiile respective...pentru ca in directia lui N1 pleaca o conducta de debit d1, iar catre N2, pleaca o conducta cu debit d2.. Desigur in care avem mai multe puncte, si acestea se continua din centrul de masa spre N2, atunci conducta va avea debitele d2 + suma debitelor nodurilor ramase..., iar Xcm,Ycm este CM-ul intregului sistem... Si se reiau calculele la fel numai ca Xcm si Ycm calculat la pasul anterior devine acum sursa... Adica poate fi facuta o functie cu parametrii ...  Oricum trebuie mai intai stabilite niste principii, de ex. Xcm si Ycm sa fie coordonatele intregului sistem de noduri, inclusiv nodul sursa, sau in calculul coordonatelor CMului sa fie luate in calcul doar nodurile cu d>D/4 ori ceva de acest gen... Apoi trebuie stabilit daca pe segmentul de dreapta ce uneste Xcm cu X'cm nu exista nici o perpendiculara pe acesta de la vreun nod... In acest caz care ar fi procedura? Fie ne oprim si mutam X'cm in acest punct si trasam de aici perpendiculara, fie lasam X'cm acolo unde cade si ne intoarcem cu o teava catre acel nod... Asta se implementeaza in algoritm si poate fi optiune de utilizator... Deci modelul matematic este putin mai complex datorita numarului de factori ce priveste eficienta costurilor care pot intreveni, si nu neaparat, de calcul geometric... De asemenea, costurile sunt iar o problema de optimizare, care pot sa dea totul peste cap, caci daca racord, manopera etc sunt foarte scumpe in raport cu teava, atunci poate e mai simplu sa trecem teava direct prin noduri si sa nu mai folosim racorduri..., folosind doar algoritmul de la calculul drumului minim.... Evident, chiar programul poate sa sugereze varianta optima dupa ce a facut o evaluare in prealabil... Daca aplicatia devine "industriala", si avem timp si motivatia  sa o complicam, putem sa folosim tot felul de algoritmi, inclusiv retele neuronale, care sa tina cont de tot felul de factori cum ar fi clima, perioada de functionare, pozitia Soarelui in momentul functionarii etc.. Ca idee e interesanta si provocatoare... Daca trebuie sa te apuci efectiv de lucru trebuie sa stabilesti din capul locului unde vrei sa te opresti... Ce pot eu sa fac acum, este sa-ti recomand niste site-uri, care e posibil sa-ti foloseasca: http://mathworld.wolfram.com/ http://www.basegroup.ru/ http://www.math.com/ Si multe altele, dar iata unul in care sunt puse in practica niste treburi interesante: http://www.liquidjourney.com/ Mai vorbim... PS: nu am pretentia ca varianta asta ar fi buna de ceva... Merita doar sa vedem de ce nu e buna, ca sa gasim alta mai buna
Acest topic a fost editat de Clopotel: 28 Jan 2006, 04:17 PM -------------------- Gandurile Mele nu sunt ca gandurile voastre si caile Mele ca ale voastre, zice Domnul.
Si cat de departe sunt cerurile de la pamant, asa de departe sunt judecatile Mele de judecatile voastre si cugetele Mele de cugetele voastre. (Isaia 55:8.9) Ortodoxia - Calea intru Hristos - pe pagina 1 indexarea tematica a subiectelor pt. o usoara urmarire... |
||||
|
|
|
||||
|
28 Jan 2006, 06:16 PM
Mesaj
#26
|
|||
|
Cronicar Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862 |
Of Clopoţel... Daca mi-ai raspunde la întrebarea pe care ţi-am pus-o, poate că am lămuri treaba. Uite, mai încerc o dată:  Ţi-e clar că algoritmul propus de tine nu descoperă varianta de cost minim?
Da, interesant. Dac-aş şti să lucrez în Flash... dar poate m-apuc acum şi învăţ. a -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
||
|
|
|
||
|
29 Jan 2006, 08:08 AM
Mesaj
#27
|
|||
|
Domnitor Grup: Membri Mesaje: 6.255 Inscris: 3 October 03 Forumist Nr.: 899 |
Simuland dinamica unui astfel de sistem de "fire grele" vei ajunge la un maxim local. Formularea problemei presupune mai mult de un maxim local (parerea mea), asftel incat o solutie de genul steepest descent/hill climbing te va baga intr-un maxim local. -------------------- Azi avem.
|
||
|
|
|
||
|
30 Jan 2006, 03:09 AM
Mesaj
#28
|
|
|
Vornic Grup: Membri Mesaje: 382 Inscris: 11 May 05 Forumist Nr.: 6.278 |
Cred ca trebuie luate in calcul urmatoarele situatii:
1. Pentru un nod simplu (sursa S, aspersoare D1(Q1) si D2(Q2), distribuitor P):  Fig.1Costul total al ansamblului este:  Fig.2Dupa cum se vede, costul depinde de cele 3 (sau 2) coordonate ale lui P (nodul intermediar). Minimul se obtine acolo unde derivatele partiale ale costului in functie de coordonate se anuleaza:  Fig.3Explicitand ecuatia costului in functie de coordonate, obtinem:  Fig.4In final, pentru conditia de minim, obtinem urmatorul sistem de ecuatii (3 ecuatii, 3 necunoscute):  Fig.52. Pentru un arbore definit topologic (pentru fiecare nod Pi este definita sursa si cele doua aspersoare care, toate pot fi noduri intermediare la randul lor): se obtine un sistem de mai multe ecuatii de genul celor din Fig.5 (cate un set pentru fiecare subansamblu - sursa, distribuitor, doua aspersoare). 3. Pentru cazul in care sunt specificate numai sursa si aspersoarele se iau in calcul toate variantele topologice de conectare a lor si pentru fiecare se aplica pct 2. Avand in vedere ca numarul variantelor creste exponential cu N (numarul aspersoarelor), problema este nedecidabila in timp rezonabil de la un N incolo. Singura problema care ramane este urmatoarea: cum se rezolva in cazul general sistemul de ecuatii din Fig 5 ?Este un sistem destul de interesant (la prima vedere)... Daca se ridica la patrat cele doua (sau trei) ecuatii si se aduna, se obtine un loc geometric petru P care nu depinde nici de S, nici de Q1 si Q2, ci numai de pozitia celor doua aspersoare. Acest topic a fost editat de bonobo: 30 Jan 2006, 03:17 AM |
|
|
|
|
30 Jan 2006, 04:22 AM
Mesaj
#29
|
|
|
Domnitor Grup: Membri Mesaje: 6.255 Inscris: 3 October 03 Forumist Nr.: 899 |
Sa presupunem ca ati reusit sa gasiti formulele pentru cazul cu o sursa si doua destinatii. Minunat. Cum extindeti solutia la o sursa si N destinatii?
Cred ca este destul de simplu de dedus ca reteaua de tevi va avea forma de arbore. Prin urmare exista setul de variabile discrete care descrie cum se construieste acel arbore (cum se partitioneaza fiecare subset = nod din arbore in subseturi mai mici = fii acelui nod, la punctele de despartire). Ce e si mai interesant este ca, pentru a afla costul la nodul curent, nu este suficient sa stii partitionarea imediata (adica daca acum ai setul de noduri active {A, B, D, E, F} si stii ca acestea se partitioneaza in {A, E} si {B, D, F}) nu poti calcula costul curent. Pentru ca punctul de despartire pentru {B, D, F} in subpartitiile corespunzatoare variaza in functie de cum partitionezi {B, D, F}. Adica presupunand ca ai un oracol care-ti spune cum sa partitionezi ACUM, nu ai cum sa determini punctul de despartire intre conducte si sa "impingi" aceasta variabila mai jos in arborele computational (care este paralel cu arborele problemei). Prin urmare exista dependenta la distanta intre variabilele continue ale solutiei (care spun pozitia nodului de despartire la conducte) - adica dependentele nu sunt doar locale (in arbore). Apropos, arborele nu este neaparat arbore binar. -------------------- Azi avem.
|
|
|
|
|
30 Jan 2006, 11:50 AM
Mesaj
#30
|
|||||
|
Cronicar Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862 |
Analiza mi se pare impecabilă. 
Da, locul geometric e suprafaţa: 0 = (x1 - x)(x2 - x) + (y1 - y)(y2 - y) + (z1 - z)(z2 - z), care se scrie mai simplu ca produsul scalar al celor doi vectori D1P şi D2P: 0 = D1P * D2P. Adică suprafaţa respectivă e locul geometric al punctelor P astfel încât segmentele PD1 şi PD2 fac unghi de 90 de grade între ele. Aceasta e exact o sferă având diametrul D1D2. (Pentru problema plană e cercul de diametru D1D2.) Rezultatul e foarte folositor, căci mai rămâne să determinăm direcţia lui SP -- dacă o ştim, soluţia sună aşa: "Pornim cu conducta groasă din S şi mergem pe direcţia 'cutare' până întâlnim suprafaţa sferei de diametru D1D2; acolo ne oprim şi despărţim conducta în două." Direcţia lui SP o putem preciza prin punctul P' care se obţine prelungindu-l pe SP până întâlneşte segmentul D1D2:  Nu am făcut calculele încă, dar soluţia va suna aşa: "În funcţie de Q1 şi Q2, determinăm un punct P' pe segmentul D1D2; pornim cu conducta groasă din S şi mergem spre acest punct P' până întâlnim suprafaţa sferei de diametru D1D2; acolo ne oprim şi despărţim conducta în două." Putem trage deja o concluzie interesantă: dacă S se află în interiorul cercului de diametru D1D2, atunci soluţia e în formă de V (conductele subţiri pornesc direct spre consumatori). O altă concluzie interesantă: privind din exteriorul cercului D1D2, cei doi consumatori pot fi "reduşi" în punctul P' (care depinde doar de debitele Q1 şi Q2 -- acest punct ar putea fi numit "centrul de debit" al celor doi consumatori). Observaţia asta cred că ne dă cheia algoritmului: reducerea succesivă a unor perechi de puncte în "centrul lor de debit"... a -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
||||
|
|
|
||||
|
30 Jan 2006, 02:24 PM
Mesaj
#31
|
|
|
Cronicar Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862 |
Grr... S-a blocat taman când postasem şi eu... Scriu din nou:
Ecuaţia o putem înmulţi cu versorii axelor şi după ce adunăm vedem că se simplifică nişte chestii şi ajungem la o ecuaţie vectorială simplă: 0 = sqrt(Q1+Q2)*versor(PS) + sqrt(Q1)*versor(PD1) + sqrt(Q2)*versor(PD2) Deci în punctul P ducem vectori către cele trei puncte, de lungimi egale cu sqrt(Q1), sqrt(Q2) şi sqrt(Q1+Q2). Aceşti trei vectori trebuie să-şi facă echilibru (suma lor să facă zero). De-aici regăsim uşor concuzia mesajului precedent: cei trei vectori respectând teorema lui Pitagora, rezultă că ei formează un triunghi dreptunghic -- deci direcţiile PD1 şi PD2 fac unghi de 90 de grade (deci P se află pe sfera/cercul de diametru D1D2). Soluţia completă este:  Adică: Desenăm cercul de diametru D1D2. Apoi, pe partea opusă lui S, construim triunghiul dreptunghic cu catete proporţionale cu sqrt(Q1), respectiv sqrt(Q2), ca în figură. Astfel determinăm punctul P'. Din S pornim cu conducta groasă către P', iar când întâlnim cercul ne oprim şi ramificăm în două conducte subţiri. Observaţie: S-ar putea ca această construcţie geometrică să ne conducă "prin spatele" unui punct (adică să întretăiem diametrul D1D2 în afara cercului). Nu e bine. În astfel de cazuri, soluţia de cost minim e următoarea: mergem cu conducta groasă până la punctul cel mai apropiat, apoi continuăm cu conductă subţire până la următorul punct (e deci un arbore degenerat). Asta e interpretarea geometrică a soluţiei pentru doi consumatori. Algoritmul general va trebui deci să grupeze consumatorii doi câte doi în diverse moduri şi să calculeze punctele P' corespunzătoare. A, şi mai trebuie făcut un lucru: să determinăm "lungimea echivalentă de conductă groasă". Adică să determinăm un punct P'', aflat pe segmentul PP', astfel încât costul unei conducte groase de la P la P'' să fie egal cu costul conductelor subţiri de la P la D1 şi la D2... a -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
|
|
|
|
30 Jan 2006, 02:25 PM
Mesaj
#32
|
|||
|
Vornic Grup: Membri Mesaje: 382 Inscris: 11 May 05 Forumist Nr.: 6.278 |
Cred ca nu am fost suficient de clar la punctul 2. Sa presupunem ca avem date: 1. pozitia sursei S(Xs, Ys, Zs) si pozitiile destinatiilor Di(Xi, Yi, Zi), i=[1..n]; 2. nodurile intermediare Pj(Sj, Dj1, Dj2), j=[1..m] (pentru nodurile intermediare se specifica numai conexiunile - sursa si cele doua destinatii - care pot fi chiar noduri intermediare la randul lor). Dupa modelul din Fig.2 se scrie expresia pentru costul arborelui: C(P1, ..., Pm) = |SP1| (Q1 + Q2 + ... + Qn)^(1/2) + ... unde Pi este dat de coordonatele (ce trebuie calculate) Xi, Yi, Zi. Deci, avem expresia costului ca fiind: C(X1, Y1, Z1, ..., Xm, Ym, Zm) = ... Apoi calculam derivatele partiale ale costului in raport cu Xi, Yi, Zi i=[1..m] si le egalam cu zero. Se obtine un sistem de 3xm ecuatii cu 3xm necunoscute: dC/dX1 = 0 dC/dY1 = 0 dC/dZ1 = 0 ... dC/dXm = 0 dC/dYm = 0 dC/dZm = 0 Se pune problema rezolvarii acestui sistem. Ecuatiile de forma dC/dUi = 0 seamana cu sistemul din Fig.5. Daca gasim o metoda de rezolvare a lui sau, mai bine, o interpretare geometrica a lui (si vad ca Amenhotep face progrese ), atunci putem spera in gasirea unei metode de rezolvare a sistemului general, si este posibil si probabil ca aceasta metoda sa fie una intuitiva, geometrica, pornind de la destinatii catre sursa.
Acest topic a fost editat de bonobo: 30 Jan 2006, 02:26 PM |
||
|
|
|
||
|
30 Jan 2006, 03:41 PM
Mesaj
#33
|
|
|
Cronicar Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862 |
Iată ce frumos arată treaba pentru trei consumatori:
 Vectorii de lungimi sqrt(Q1), sqrt(Q2) şi sqrt(Q3) trebuie să-şi facă echilibru cu vectorul sqrt(Q1+Q2+Q3), ca în figură. Lungimile lor sunt date de debite şi ei trebuie să-şi găsească unghiurile încât să se echilibreze. Echilibrarea cred că se poate face simplu, cu un algoritm care să simuleze efectiv procesul dinamic prin care sistemul tinde la echilibru. În cel mai rău caz, trebuie generaţi toţi arborii... a EDIT: Am testat soluţia geometrică pentru trei puncte şi am găsit că pot fi construiţi ambii arbori încât să respecte cerinţele algoritmului geometric! Asta înseamnă că geometria nu ne poate ajuta să decidem structura arborelui. Deci trebuie efectiv încercaţi toţi. Păcat, speram ca soluţia geometrică să ne scutească de aşa ceva... Acest topic a fost editat de Amenhotep: 30 Jan 2006, 05:47 PM -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
|
|
|
|
31 Jan 2006, 04:16 PM
Mesaj
#34
|
|||
|
Cronicar Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862 |
Nu cred că e corect. Pentru 3 noduri sunt într-adevăr doar 3 variante, conform formulei 2^(N-1) - 1: (ab)c (ac)b (bc)a Pentru 4 noduri, formula 2^(N-1) - 1 dă 7. Dar numărând efectiv modurile de grupare găsim 15 variante: (ab)(cd) (ac)(bd) (ad)(bc) ((ab)c)d ((ac)b)d ((ad)b)c ((bc)a)d ((bd)a)c ((cd)a)b ((ab)d)c ((ac)d)b ((ad)c)b ((bc)b)a ((bd)c)a ((cd)b)a Deci formula nu e bună. Eu gândesc aşa: Să numărăm segmentele (ramurile). Pentru N = 2, avem trei segmente (şi un singur arbore posibil). Adăugând un nod suplimentar, vedem că el se poate "grefa" pe oricare din cele trei segmente -- deci pentru N = 3 vor rezulta 3 arbori distincţi. Cum grefarea unui nod pe un segment transformă acel segment în trei segmente, înseamnă că numărul de segmente a devenit acum 3 + 2 = 5. Deci pentru N = 3 avem 3 arbori distincţi, fiecare cu câte 5 segmente. Un al patrulea nod se poate grefa orinde pe aceste segmente, deci vor fi 15 variante. Şi tot aşa: segmente[2] = 3; arbori[2] = 1 segmente[3] = segmente[2] + 2; arbori[3] = arbori[2] * segmente[2] ... segmente[N+1] = segmente[N] + 2; arbori[N+1] = arbori[N] * segmente[N] Rezultă: segmente[N+1] = 2*N + 1; arbori[N+1] = (2*N)! / N! / 2^N (produsul numerelor impare de la 1 la 2*N-1) Iată deci că numărul de arbori creşte mult mai repede: de exemplu, pentru 7 noduri, formula lui Cătălin dă 63, pe când formula de-aici dă 10395 de variante!) a -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
||
|
|
|
||
|
8 Feb 2006, 04:49 PM
Mesaj
#35
|
|
|
Cronicar Grup: Moderator Mesaje: 2.132 Inscris: 16 June 04 Din: Bucuresti Forumist Nr.: 3.862 |
Am implementat algoritmul! (Cu echilibrul celor trei vectori proporţionali cu radical din Q.) În Flash (da, am învăţat Flash -- e mult mai simplu decât credeam; Clopoţel, ţie-ţi datorez imboldul!
).Funcţionează admirabil şi rezultatele sunt spectaculoase (a durat 4 ore să fac programul şi apoi vreo alte 12 ore am stat privind cum optimizează diverşi arbori generaţi aleatoriu; e addictive, zău!). Din păcate fişierul Flash nu-l pot ataşa pe server, că nu acceptă fişiere Flash. Iată mai jos un exemplu de arbore final, echilibrat:  Punctele verzi sunt frunze (fixate la inceput), iar cele roşii sunt nodurile intermediare a căror poziţie o determină algoritmul. Din păcate, aşa cum a zis şi Axel, se ajunge doar la un minim local. Asta înseamnă că soluţiile găsite nu sunt garantat optime, ci e posibil să fie doar nişte minime locale: orice mică deviaţie într-adevăr ar creşte costul total, dar o mare deviaţie (deci o schimbare drastică de configuraţie) ar conduce la un cost încă şi mai mic. Am verificat asta punând în program un buton care-mi permite să las frunzele pe loc şi să restartez algoritmul pornind de la o altă distribuţie aleatoare a nodurilor roşii -- şi se vede cum uneori algoritmul găseşte o soluţie încă mai bună decât cea pe care-o găsise iniţial. Mă gândesc să fac o chestie gen "călire simulată" -- adică să "zgâlţâi" puternic arborele la început, reducând treptat intensitatea zgâlţâielilor în timp. (De fapt, chiar şi acum apare un fenomen de genul ăsta, numai că e o consecinţă surprinzătoare a algoritmului, nu e proiectată voit de mine). Cine vrea să vadă programul să-mi scrie pe PM şi să-mi dea o adresa de e-mail unde să i-l trimit (are doar 2 KB!). a -------------------- Trebuie să facem ceea ce credem că e bine, dar nu trebuie să credem că ceea ce facem e bine.
|
|
|
|
|
|
Versiune Text-Only | Data este acum: 10 November 2024 - 09:46 PM |